
Since the advent of quantum computing, there has been a certain shift on the perception of how we treat data. Quantum algorithms, in a sense, may allow to bypass some value-checking we may label as essential. Two quantum phenomena mainly form the basis of this logical shift: entanglement, which allows data points to have multiple values, and quantum interference, which allows the data points to influence each other1. This interdependency permits, via clever tricks in algorithm-making which algorithm designers are certainly used to, a sizeable reduction in time and space used for computation.
THE DEUTSCH-JOSZA PROBLEM
The Deutsch algorithm, later generalized by Josza, as Mr. Alastair Abbott of the University of Auckland describes it2, “is one of the most basic ways to demonstrate the power of quantum computation.” Since it still involves a lot of mathematics, we will try and reduce it to a non-mathematical, more physical problem. As this blog post is destined to make non-technical explanations, we will use the age-old metaphorization through red and blue balls, and coins: let us say we possess 2 coins, one silver, one gold. In front of us stands a machine, which, upon being fed a coin, drops a ball, which can be either blue or red. What we want to know is this: will (a) both coins give a ball of the same color, of will we (b) receive a differently colored ball for each coin? Obviously, for a classical computer, one would have to put both coins in order to tell with certainty whether the machine is in the (a) or (b) configuration.
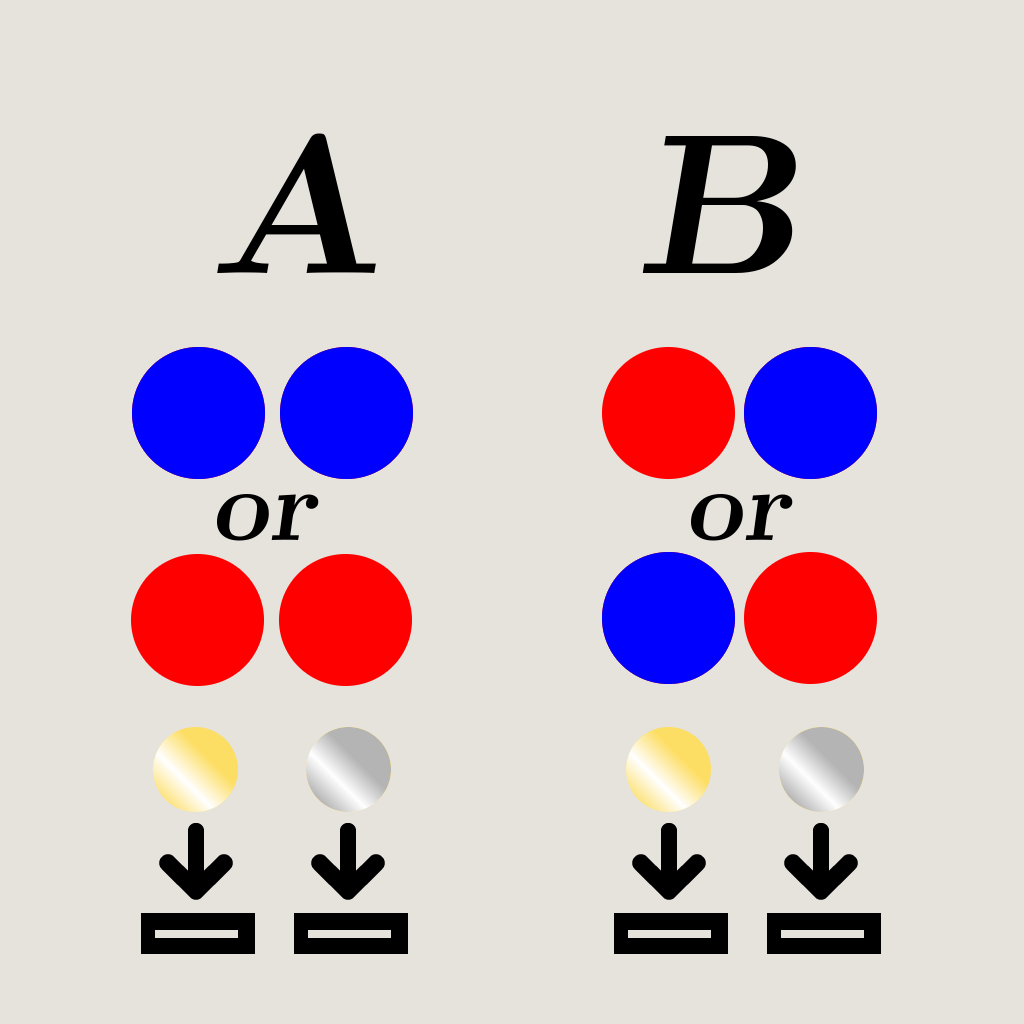
MAKING A QUANTUM ALGORITHM
The Deutsch algorithm uses the peculiarities of quantum mechanics in order to solve this using only one coin. Let us now describe the two objects which we will use to build our quantum algorithm.
First, the f-controlled-NOT gate, or f-c-n, which is mostly a series of actions. When we go through this gate, we insert a first coin into the machine; if we get a red ball, we swap the leftover coin with a silver one if gold, and a gold one if silver. If we get a blue ball, nothing happens. This gate is not an inherently quantum process; the relevant part is that it counts as one coin being used.
Secondly, the Hadamard gate, which may be pictured as a coin-modifying tool. When we use this tool on a coin, it turns into a mathematical combination of silver and gold, which, for simplicity’s sake, we will not specify. Its two main characteristics are that the modified coin has a 50/50 chance of being either gold or silver when we look at it, and that using the Hadamard gate twice on a coin will return it to a definite composition. This gate is intrisic to quantum computing, it is one of its inherent tools which researchers can use.
Then, what happens when we first modify a coin, and then put it through a f-c-n gate? Without going through the mathematics, intuition tells us that if the coin is not definitely gold or silver, and that it goes through the machine, it somehow probes both results at once. Formally, the Deutsch algorithm consists of one Hadamard gate on both coins, then the f-c-n gate on one coin, then another Hadamard gate on both coins. The results are clear: when we look at our leftover coin, it has returned to a definite composition, and it will have changed according to whether the machine follows situation (a) or (b). Furthermore, as we have stated before, the f-c-n gate counts as one operation of the machine, and therefore, we have managed to find the solution without using both of our coins.
The Deutsch algorithm is known to have helped grow the interest in the field and led to more complex quantum algorithms, such as Shor’s algorithm. While the strengths of quantum computing are undeniable, it may be a strange process to learn anew how one and zeros may evolve.
1. Cleve, R., et al. “Quantum Algorithms Revisited.” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 454, no. 1969, The Royal Society, Jan. 1998, pp. 339–354. Crossref, doi:10.1098/rspa.1998.0164.
2. Abbott, A. A. “The Deutsch–Jozsa Problem: De-quantisation and Entanglement, 2009.” arXiv preprint arXiv:0910.1990.
