
Depuis l’avènement de l’informatique quantique, il y a eu un certain changement dans la perception de la façon dont nous traitons les données. Les algorithmes quantiques, dans un sens, peuvent permettre de contourner certains contrôles de valeur que nous pouvons étiqueter comme essentiels. Deux phénomènes quantiques constituent principalement la base de ce changement logique : l’enchevêtrement, qui permet aux points de données d’avoir des valeurs multiples, et l’interférence quantique, qui permet aux points de données de s’influencer les uns les autres1. Cette interdépendance permet, grâce à des astuces astucieuses dans la fabrication d’algorithmes auxquels les concepteurs d’algorithmes sont certainement habitués, une réduction importante du temps et de l’espace utilisés pour le calcul.
LE PROBLÈME DEUTSCH-JOSZA
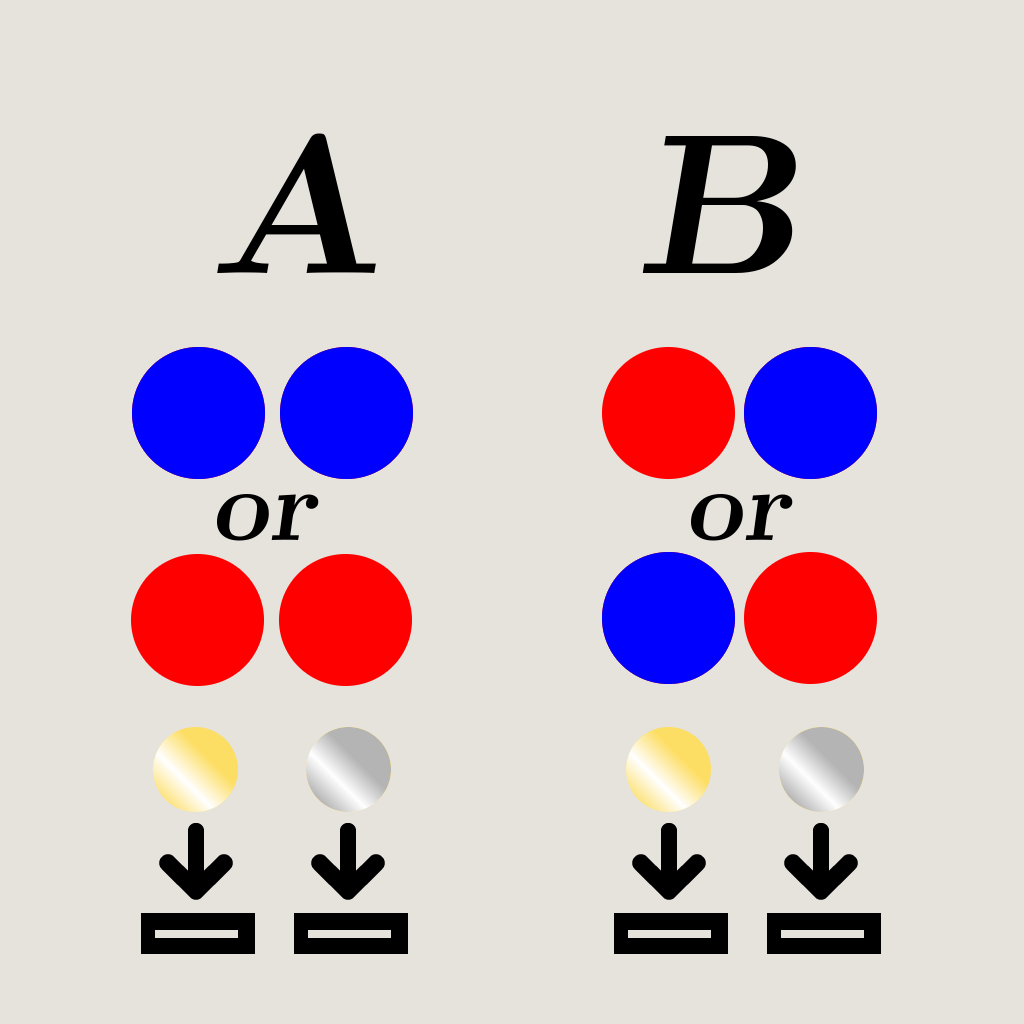
L’algorithme Deutsch, plus tard généralisé par Josza, comme le décrit M. Alastair Abbott de l’Université d’Auckland2, « est l’un des moyens les plus élémentaires de démontrer la puissance du calcul quantique ». Comme il implique encore beaucoup de mathématiques, nous allons essayer de le réduire à un non-mathématique, plus de problème physique. Comme ce billet de blog est destiné à faire des explications non techniques, nous allons utiliser la métaphore séculaire à travers des boules rouges et bleues, et des pièces de monnaie: disons que nous possédons 2 pièces de monnaie, une argent, une or. En face de nous se tient une machine, qui, après avoir été nourri une pièce de monnaie, laisse tomber une balle, qui peut être soit bleu ou rouge. Ce que nous voulons savoir, c’est si on va (a) recevoir une balle de la même couleur, ou (b) recevoir une balle de couleur différente pour chaque pièce? Évidemment, pour un ordinateur classique, il faudrait mettre les deux pièces pour dire avec certitude si la machine est dans la configuration (a) ou (b).
MAKING A QUANTUM ALGORITHM
L’algorithme Deutsch utilise les particularités de la mécanique quantique afin de résoudre ce problème en utilisant une seule pièce. Décrivons maintenant les deux objets que nous utiliserons pour construire notre algorithme quantique.
Tout d’abord, la porte f-control-NOT, ou f-c-n, qui est principalement une série d’actions. Lorsque nous passons par cette porte, nous insérons une première pièce dans la machine; si nous obtenons une boule rouge, nous échangeons la pièce de monnaie restante avec une en argent si c’était l’or, et inversement. Si on a une balle bleue, il ne se passe rien. Cette porte n’est pas un processus intrinsèquement quantique; la partie pertinente est qu’elle compte comme une pièce utilisée.
Deuxièmement, la porte Hadamard, qui peut être représenté comme un outil de modification de pièces de monnaie. Lorsque nous utilisons cet outil sur une pièce de monnaie, il se transforme en une combinaison mathématique d’argent et d’or, que, pour l’amour de la simplicité, nous ne spécifierons pas. Ses deux principales caractéristiques sont que la pièce modifiée a une chance de 50/50 d’être soit d’or ou d’argent quand nous la regardons, et que l’utilisation de la porte Hadamard deux fois sur une pièce de monnaie la ramènera à une composition définie. Cette porte est intrisèque à l’informatique quantique, c’est l’un de ses outils inhérents que les chercheurs peuvent utiliser.
Ensuite, que se passe-t-il lorsque nous modifions d’abord une pièce de monnaie, puis la mettons à travers une porte f-c-n? Sans passer par les mathématiques, l’intuition nous dit que si la pièce n’est pas définitivement d’or ou d’argent, et qu’il passe par la machine, il sonde en quelque sorte les deux résultats à la fois. Officiellement, l’algorithme Deutsch se compose une porte Hadamard sur les deux pièces, puis la porte f-c-n sur une pièce, puis une autre porte Hadamard sur les deux pièces. Les résultats sont clairs: quand nous regardons nos pièce restantes, on est revenu à une composition définie, et qui aura changé selon que la machine suit la configuration (a) ou (b). En outre, comme nous l’avons déjà dit, la porte f-c-n compte comme une seule opération de la machine, et par conséquent, nous avons réussi à trouver la solution sans utiliser nos deux pièces.
L’algorithme Deutsch est connu pour avoir contribué à développer l’intérêt dans le domaine et a conduit à des algorithmes quantiques plus complexes, tels que l’algorithme de Shor. Bien que les forces de l’informatique quantique soient indéniables, il peut être étrange d’apprendre à nouveau comment un et zéro peuvent évoluer.
1. Cleve, R., et coll. « Algorithmes quantiques revisités. » Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 454, no. 1969, The Royal Society, janv. 1998, pp. 339-354. Crossref, doi:10.1098/rspa.1998.0164.
2. Abbott, A. A. « The Deutsch-Jozsa Problem: De-quantisation and Entanglement, 2009. » arXiv preprint arXiv:0910.1990.
